머신러닝을 위한 수학 시리즈는 머신러닝을 이해하기 위한 수학을 A 부터 Z까지 설명하는 포스트가 아닙니다. 저 또한 머신러닝을 공부하면서 머신러닝을 이해하기 위해 필요한 최소한의 수학 개념을 정리한 것 뿐입니다. 이번 포스트에서는 그 중에 미분, 편미분, 시그모이드 함수, 로그 함수의 개념에 대해서 정리하였습니다.
미분, 로그 함수만 정규과정 중에 배웠던 기억이 나네요….; 미분, 로그 함수 뿐만 아니라 편미분과 시그모이드 함수에 대해서도 간략하게 정리해 보았습니다.
미분
미분은 함수에서 한 지점에서의 변화율을 나타내는 수학적인 개념입니다. 간단히 말해서, 함수의 입력값이 조금만 변할 때 함수 값이 얼마나 변하는지를 나타냅니다. 이는 함수의 그래프에서 한 점에서의 기울기(미분 계수)를 의미합니다.
한 점에서의 기울기를 구하기 전에 두 점 사이의 기울기를 구해보겠습니다.
A(a, f(a)), B(b, f(b))에 해당하는 두 점 사이 기울기는 다음과 같이 표현 될 수 있습니다.
$$\frac{y값의 증가량}{x값의 증가량} = \frac{f(b) – f(a)}{b – a} = \frac{f(a + \Delta x) – f(a)}{\Delta x}$$
이와 같은 직선 AB의 기울기를 A와 B 사이의 ‘평균 변화율’이라고 부릅니다.
미분은 한 지점에서의 변화율이기 때문에 ‘순간 변화율’을 구해야 합니다.
순간 변화율은 x의 증가량이 0에 가까울 만큼 아주 작을 때의 순간적인 기울기를 말합니다.
이를 극한(lim) 기호를 사용해 다음과 같이 나타낼 수 있습니다.
$$f'(x) = \lim_{{\Delta x \to 0}} \frac{{f(a+\Delta x) – f(a)}}{\Delta x}$$
편미분
하나의 변수가 아니라 여러가지 변수가 식 안에 있을 때, 모든 변수를 미분하는 것이 아니라 우리가 원하는 한 가지 변수만 미분하고 그 외에는 모두 상수로 취급하는 것이 바로 편미분 입니다.
다음 식과 같이 x, y 두 개의 변수가 있을 때 어떤 변수로 미분해야 하는지 정해야 하므로 편미분을 사용합니다.
$$f(x,y) = x^2 + yx +a$$
함수 f를 “x에 관해 편미분 하라“고 하면 다음과 같은 식을 씁니다.
$$\frac{\partial y}{\partial x}$$
편미분은 미분하는 변수가 아니면 다른 모든 항을 상수로 취급합니다.
따라서 아래 예제 식에서 y는 상수로 취급됩니다.
$$f(x,y) = x^2 + xy + a$$
위 식을 x에 관해 미분하면 아래와 같이 됩니다.
$$\frac{\partial y}{\partial x} = 2x + y$$
시그모이드 함수
시그모이드 함수는 입력값을 0과 1 사이의 값으로 변환하는 특징 때문에 주로 이진 분류 문제에서 사용됩니다.
자연 상수 e가 지수 함수에 포함되어 분모에 들어가면 시그모이드 함수가 됩니다.
시그모이드 함수는 다음과 같이 표현됩니다.
$$f(x) = \frac{1}{1+e^-x}$$
자연 상수 e는 ‘자연 로그의 밑’, ‘오일러의 수’ 등 여러 이름으로 불립니다.
그 값은 대략 2.718281828… 입니다.
시그모이드 함수를 그래프를 그려보면 아래와 같이 S자 형태로 나타납니다.
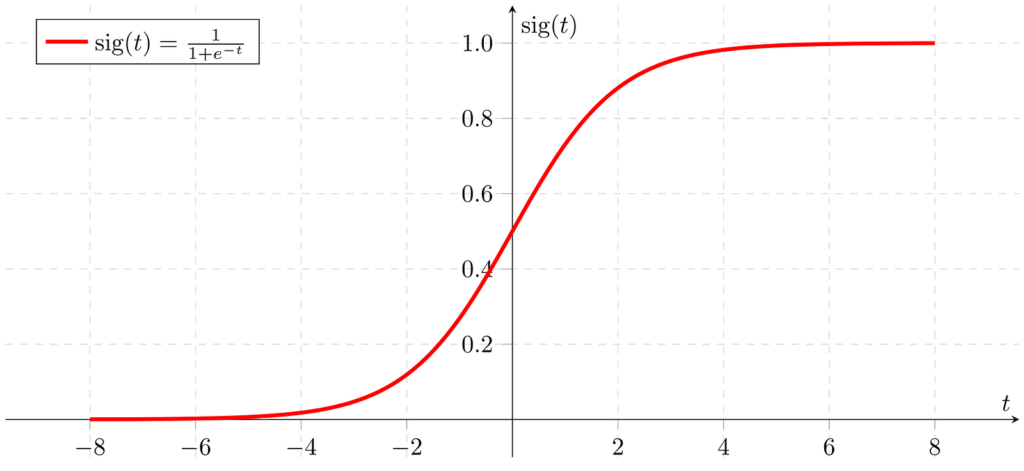
로그 함수
로그 (Logarithm)는 지수 개념을 먼저 이해해야 합니다. a를 x만큼 거듭제곱한 값이 b라고 할 때, 아래와 같이 나타낼 수 있습니다.
$$a^x = b$$
이때 a와 b는 아는데 x를 모른다고 할 때, x를 구하기 위해 사용하는 방법이 로그 입니다.
로그는 지수 식에서 위치를 바꿔서 아래와 같이 나타냅니다.
$$\log_{a}(b) =x$$
로그 함수는 지수 함수와 역함수 관계 입니다. 역함수 그래프는 y=x 에 대해서 대칭인 선으로 나타납니다.
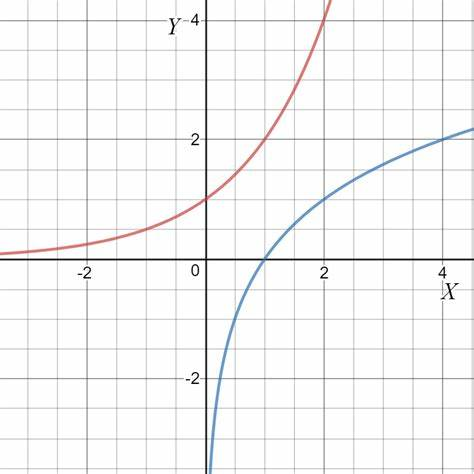
로지스틱 회귀를 공부할 때, x가 1에 가까워지거나, 0에 가까워질수록 오차가 커지는 그래프가 필요합니다. 이러한 그래프를 만들 때 로그함수를 이용합니다.
