머신러닝을 위한 수학 시리즈는 머신러닝을 이해하기 위한 수학을 A 부터 Z까지 설명하는 포스트가 아닙니다. 저 또한 머신러닝을 공부하면서 머신러닝을 이해하기 위해 필요한 최소한의 수학 개념을 정리한 것 뿐입니다. 이번 포스트에서는 그 중에 선형 회귀, 최소 제곱법, 평균 제곱 오차의 개념에 대해서 정리하였습니다.
선형 회귀 모델은 이전에 바이러스의 titration을 진행 할 때 개인적으로 사용해보았습니다.
하지만 최소 제곱법과, 평균 제곱 오차는 생소한 개념입니다…
이들은 무엇이고 어디에 쓰이는 것일까요?
<안물안궁. 바이러스 titration을 위해 qPCR 데이터와 선형 회귀 모델을 사용하는 법>
- qPCR을 사용하여 먼저, 정확히 알려진 바이러스 양에 대한 Ct값을 정리하고 이를 기반으로 선형 회귀 모델을 만듭니다.
- 선형 회귀 모델의 성능을 평가하기 위해 $R^2$값을 검사합니다.
- 이후 구축한 선형 회귀 모델을 사용하여 미지의 바이러스 샘플에 대한 Ct값으로부터 해당 바이러스의 양을 예측합니다.
선형 회귀 (Linear regression)
선형 회귀는 쉽게 풀어서 정의하면 가장 훌륭한 예측선 긋기 입니다.
우선 식물을 예를 들어보겠습니다. 만일 식물이 30시간의 햇빛을 쬐니까 35cm가 되었고 40시간을 쬐니까 48cm가 되고 50시간을 쬐니까 67cm가 되고 60시간을 쬐니 74cm가 되었다고 가정해보겠습니다.
여기서 햇빛을 쬔 시간(일조량)을 x축으로 하고 식물의 길이를 y축으로 하면 아래와 같이 나타낼 수 있습니다.
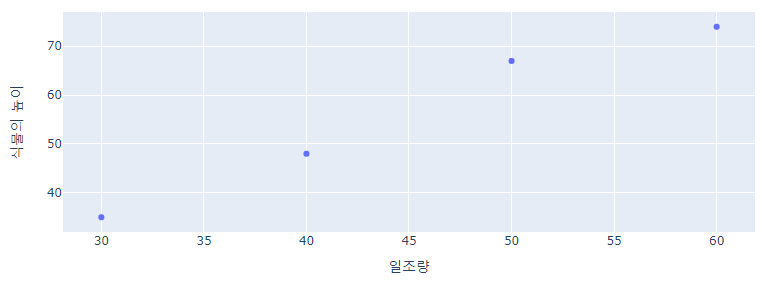
평면에 나타내 놓고 나니, 왼쪽에서 오른쪽으로 우상향 되는 선형 형태로 점이 찍힌 것을 확인 할 수 있습니다.
선형 회귀는 이 점들의 특징을 가장 잘 나타내는 선을 그리는 과정입니다.
최소 제곱법 (Least Squares Method)
위에서 선형 회귀는 점들의 특징을 잘 나타내는 선을 그리는 과정이라고 묘사했습니다.
여기서 선은 직선이므로 일차 함수 그래프로 나타낼 수 있습니다.
$$y = ax + b$$
여기서 a, b를 구해야 하는데 a와 b를 실제 데이터에 가장 적합하게 구하는 것이 핵심 목표입니다.
최소 제곱법이라는 공식을 알고 있으면 오차를 최소화하는 방향으로 a, b를 구할 수 있습니다.
아래가 최소 제곱법을 사용하여 기울기 a를 구하는 방법입니다.
$$a = \frac{(x – x평균)(y – y평균)의 합}{(x – x평균)^2의 합}$$
같은 공식을 조금 더 수학적으로 표현하면 아래와 같습니다.
$$a = \frac{\sum_{i=1}^{n}(x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^{n}(x_i – \bar{x})^2}$$
위에서 예시를 든 일조량과 식물의 높이를 최소 제곱법으로 구하면 a = 1.36이 됩니다.
y 절편 b는 아래의 공식으로 구합니다.
$$b = y의 평균 – (x의 평균 * 기울기 a)$$
같은 공식을 조금 더 수학적으로 표현하면 아래와 같습니다.
$$b = \bar{y} – (\bar{x} * a)$$
위의 공식을 사용하면 b = -5.200000000000003이 나옵니다.
이제 예측 값을 구하기 위한 직선의 방정식이 아래와 같이 완성되었습니다.
$$y = 1.36x+ -5.200000000000003$$
이제 방정식에 우리가 가진 일조량 데이터를 대입하면 아래와 같은 예측 값을 구할 수 있습니다.
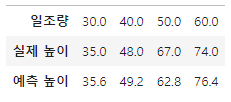
실제 값을 파란점, 최소 제곱법으로 나온 방정식으로 예측값을 찍으면 빨간점으로 표기하면 아래와 같은 그래프를 확인 할 수 있습니다.
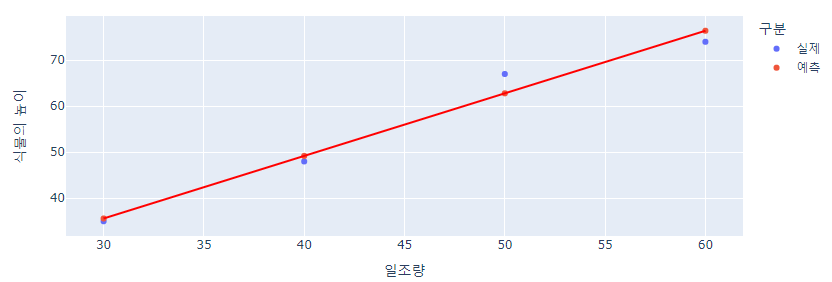
최소 제곱법 파이썬 코딩
위의 절차를 파이썬으로 코딩하면 아래와 같습니다.
# 일조량 리스트
sun_hour = [30, 40, 50, 60]
# 식물의 높이 리스트
plant_height = [35, 48, 67, 74]
# 평균 일조량
mean_sun = np.mean(sun_hour)
# 평균 식물의 높이
mean_plant = np.mean(plant_height)
# (x - x평균)^2의 합
divisor = sum([(i - mean_sun)**2 for i in sun_hour])
# (x - x평균)(y - y평균)의 합
dividend = 0
for i in range(len(sun_hour)):
dividend += (sun_hour[i] - mean_sun)*(plant_height[i] - mean_plant)
# 최소 제곱법
a = dividend / divisor
# 평균 식물의 높이 - (평균 일조량 * a)
b = mean_plant - (mean_sun * a)평균 제곱 오차 (Mean Squared Error, MSE)
앞서 최소 제곱법으로 기울기와 절편을 편하게 구했지만, 이 공식만으로 모든 상황을 해결하기는 어렵습니다.
여러 개의 입력을 처리하기에는 무리가 있기 때문 입니다.
여러 개의 입력값을 계산할 때는 임의의 선을 그리고 난 후, 이 선이 얼마나 잘 그려졌는지 평가하여 조금씩 수정해 나가는 방법을 사용합니다.
이를 위해 주어진 선의 오차를 평가하는 오차 평가 알고리즘이 필요합니다.
평균 제곱 오차, 평균 절대 오차 등이 있지만 평균 제곱 오차가 가장 많이 사용 됩니다.
평균 제곱 오차는 말 그대로
오차(실제 값과 예측 값 사이의 차이), 제곱(오차의 제곱), 평균(오차 제곱들의 평균)를 의미합니다.
수식으로 표현하면 아래와 같습니다.
$$MSE = \frac{\sum_{i=1}^{n}(y_i – \hat{y_i})^2}{n}$$
마치며
선형 회귀는 앞서 가장 훌륭한 예측선 긋기이라고 표현했는데요.
이 과정을 풀어서 설명하면 “임의의 직선을 그어 이에 대한 평균 제곱 오차를 구하고, 이 값을 가장 작게 만들어 주는 a와 b 값을 찾아가는 작업” 이라고 할 수 있습니다.
위에서는 선형 회귀의 개념을 설명하고 선형 회귀 공식을 구하기 위한 방법만 다루었는데요.
선형 회귀를 제대로 알기 위해서는 단순 선형 회귀 외에도 여러 선형 회귀와, 선형 회귀에서의 가정, 경사하강법 등 개념을 추가적으로 공부해야 할 것 같습니다… ㅎ
해당 개념도 곧 공부해서 정리해보도록 하겠습니다
