들어가며
이전에 가장 기초적인 데이터 분할 방법인 “홀드아웃”에 대해서 정리해보았습니다. 이번에는 “홀드아웃”에서의 단점인 오버피팅 및 떨어지는 일반화 성능을 개선한 “K-fold 교차검증” 방법에 대해 공부해보았습니다.
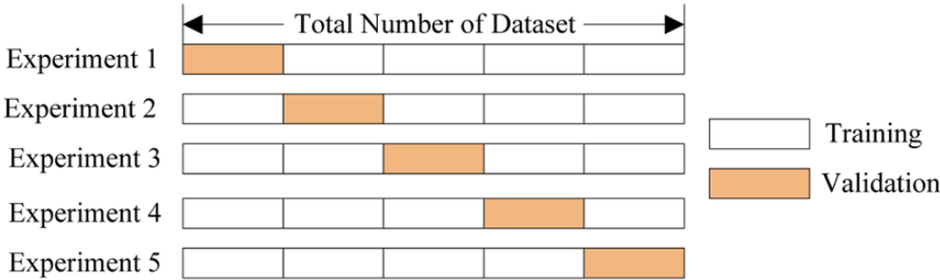
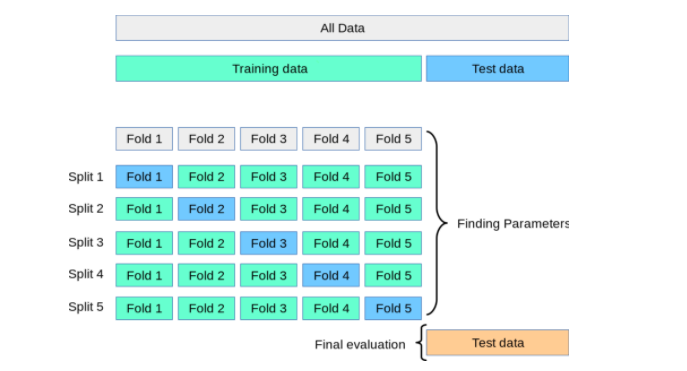
왼쪽 그림은 제가 k-fold cross validation 개념을 처음 배웠을 때 이를 설명하던 그림 입니다. 하지만 이 그림만 보아서는 K-fold 교차검증이 정확히 무엇인지 이해하기 어려울 수 있습니다.
때문에 해외 블로그들을 방문하며 K-fold Cross-validation이란 무엇인지 공부해보았습니다.
K-fold 교차검증
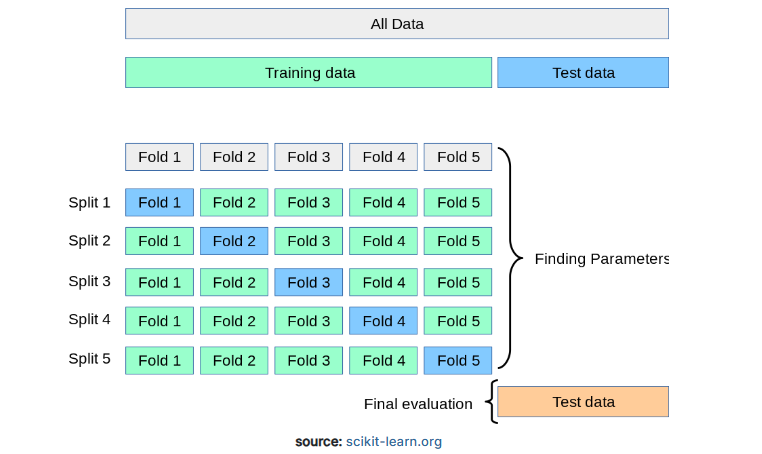
위 그림은 k-fold cross validation을 제대로 설명해주고 있습니다. “K-fold cross validation”이 무엇인지 아래 설명과 함께 보시면 제대로 이해 하실 수 있습니다.
K-fold cross validation 방법은 데이터세트를 동일한 크기의 k개 fold로 나눕니다.
그리고 훈련에는 k-1 fold를 사용하고 검증에 1 fold를 사용하여 모델을 k번 반복적으로 훈련하는 겁니다.
K-fold cross-validation을 사용하면 k개의 서로 다른 데이터 세트에서 모델을 “테스트”할 수 있으며, 이는 모델이 일반화 가능한지 확인하는 데 도움이 됩니다.
이 기술은 모든 데이터를 사용하여 모델을 학습할 때 발생할 수 있는 과적합을 방지하는 데 도움이 되기 때문에 사용됩니다.
이 기술은 데이터가 부족한 경우에 사용하면 좋습니다.
K-fold 교차검증 프로세스
- 데이터 세트는 훈련 데이터 세트와 테스트 데이터 세트로 분할됩니다.
- 그런 다음 훈련 데이터 세트를 K-fold로 분할합니다.
- K-fold 중 (K-1)fold를 학습에 사용
- 1 fold는 validation에 사용됩니다.
- 특정 초매개변수가 있는 모델은 훈련 데이터(K-1 fold)와 검증 데이터를 1 fold로 사용하여 훈련됩니다. 모델의 성능이 기록됩니다.
- 위의 단계(3단계, 4단계, 5단계)는 각 k-fold가 검증 목적으로 사용될 때까지 반복됩니다. 이것이 k-fold 교차 검증이라고 불리는 이유입니다.
- 마지막으로, 각 K 모델에 대해 5단계에서 계산된 모든 모델 점수를 취하여 모델 성능의 평균 및 표준편차를 계산합니다.
- 서로 다른 하이퍼파라미터 값에 대해 3단계부터 7단계까지 반복됩니다.
- 마지막으로, 가장 최적의 평균과 모델 점수의 표준편차를 생성하는 하이퍼파라미터가 선택됩니다.
- 그런 다음 전체 훈련 데이터 세트를 사용하여 모델을 훈련하고(2단계) 테스트 데이터 세트에서 모델 성능을 계산합니다(1단계).
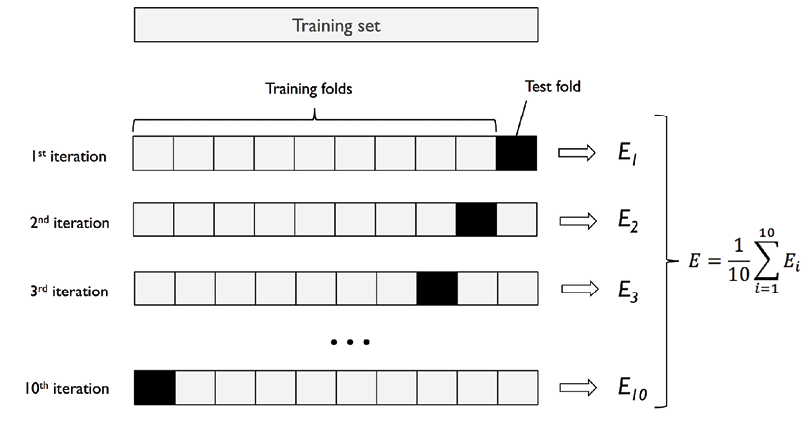
K-fold 교차검증 방법의 예
이해를 돕기 위해 1000개의 샘플로 k-fold 교차 검증을 진행한다면 어떻게 데이터가 분할되고 테스트 되는지 아래 설명을 참고하면 좋습니다.
1000개의 샘플로 구성된 데이터 세트가 있고 k=5인 k-겹 교차 검증을 사용한다고 가정합니다.
데이터 세트는 먼저 80:20 분할 비율을 기준으로 훈련 및 테스트 데이터 세트로 분할 됩니다.
따라서 훈련 목적으로 800개의 레코드가 있습니다.
훈련 데이터 세트(800개 레코드)는 각각 160개 샘플의 5개 하위 세트로 분할됩니다.
그런 다음 이러한 하위 집합 중 4개(640 개 레코드)에 대해 모델을 훈련하고 나머지 하위 집합(160개 레코드)으로 성능을 평가합니다.
이 프로세스는 5번 반복되며, 160개 샘플의 각 하위 집합은 정확히 한 번씩 검증 데이터로 사용됩니다.
그런 다음 이 5가지 평가의 결과와 표준편차를 계산하여 해당 모델에 대한 평가 지표를 생성합니다.
이 프로세스는 다양한 하이퍼파라미터에 대해 반복됩니다.
그런 다음 서로 다른 모델의 평균과 표준편차를 비교하여 전체 모델 중에서 하나의 모델을 선택합니다.
특정 하이퍼파라미터와 알고리즘을 갖춘 새로운 모델은 전체 800개의 레코드에 대해 훈련되고 따로 보관된 200개의 레코드에 대해 테스트됩니다.
최종 모델은 특정 알고리즘과 하이퍼파라미터를 이용해서 훈련 데이터 모두를 훈련하여 모델을 만드는 것에 주목합니다.
K-fold 교차검증이 사용되는 시나리오
하이퍼파라미터 튜닝
K-fold 교차검증을 사용하여 모델의 하이퍼파라미터를 튜닝할 수 있습니다.
하이퍼파라미터의 예로는 학습률 (learning rate), 정규화 매개변수 (regularization parameter), 신경망의 숨겨진 레이어(hidden layers) 수가 있습니다.
K-fold 교차검증은 다양한 하이퍼파라미터 설정에서 모델의 성능을 평가하고 최상의 성능을 제공하는 최적의 하이퍼파라미터를 선택하는 데 사용할 수 있습니다.
모델 선택
K-fold 교차 검증을 사용하여 후보 모델 집합 중에서 가장 적합한 모델을 선택할 수 있습니다.
여기에는 훈련 데이터의 k-1 하위 집합에 대해 각 모델을 훈련하고 나머지 하위 집합에 대한 성능을 평가하는 작업이 포함됩니다.
검증 데이터에서 가장 좋은 성능을 보이는 모델이 최종 모델로 선택됩니다.
데이터 전처리
K-fold 교차검증을 사용하여 다양한 데이터 전처리 기술이 모델 성능에 미치는 영향을 평가할 수도 있습니다.
예를 들어, 다양한 정규화 기술을 사용하여 정규화 된 데이터세트에서 모델의 성능을 평가할 수 있습니다.
K 값 결정하기
K의 스탠더드 값은 10이며 적당한 크기의 데이터에 사용됩니다.
매우 큰 데이터 세트의 경우 K 값을 5로 사용할 수 있습니다.
K값을 줄이는 경우, 모델을 refitting 하고 다양한 fold에서 모델을 평가하는 데 드는 계산 비용을 줄이면서 모델의 평균 성능에 대한 정확한 추정치를 얻을 수 있습니다.
데이터가 상대적으로 작을수록 fold 수를 늘립니다. 각 훈련 fold의 크기가 더 작아지기 때문에 이 모델 성능은 더 높은 분산으로 추정 될 수 있습니다.
K-fold 교차 검증의 단점
k-fold 교차 검증의 단점은 실행 속도가 느리고 병렬화가 어려울 수 있다는 것입니다.
또한 다음 시나리오 중 일부에서는 k-fold 교차 검증이 최선의 옵션은 아닙니다.
분류 문제에 불균형한 데이터 세트가 있고 target 수준과 featrue 수준 모두에서 소규모 클래스의 비율을 보존해야 하는 경우
- 예를 들어 사기 감지, 스팸 감지 등이 있습니다.
- 이 경우 솔루션은 stratified k-fold을 이용하는 것 입니다.
- stratified k-fold 교차 검증에서는 보존하려는 분포를 유지하는 제어된 방식으로 샘플링이 수행됩니다.
- Sklearn의 StratifiedKFold를 사용할 수 있습니다.
- 다중 라벨 분류의 경우 Scikit-multilearn 패키지(http://scikit.ml/)를 사용할 수 있습니다.
- multilearn 패키지에서 사용되는 반복 계층화 (iterative stratification)에 대해 알아보려면 다음 논문을 참조할 수도 있습니다.
- On the stratification of multi-label data. Machine Learning and Knowledge Discovery in Databases
회귀 문제에 불균형한 데이터 세트가 있고 target 수준과 feature 수준 모두에서 숫자 변수의 분포를 보존해야 하는 경우
- 이 경우 솔루션은 마찬가지로 stratified k-fold 가 될 수 있습니다.
- 회귀 문제로 계층화를 달성하기 위해 Pandas
cut방법을 사용할 수 있습니다.
시계열 예측과 같이 독립적이지 않고 동일하게 분포된(non-i.i.d) 사례를 처리하는 경우
- 모든 데이터 포인트는 독립적이며 동일하게 분포됩니다. 그러나 시계열 데이터에서 관측치는 일반적으로 이전 관측치에 따라 달라집니다.
- 이러한 시간적 의존성은 데이터를 무작위 fold로 분할하면 시간적 순서가 깨져버립니다.
- 이런 경우, 미래 데이터로 모델을 훈련하고 과거 데이터로 테스트를 진행하는 것과 같은 편향이 생길 수 있습니다.
- 이 경우, 해결책은 Sklearn의 GroupKFold를 사용하는 것입니다. 또 다른 접근 방식은 Sklearn의 TimeSeriesSplit을 사용하는 것입니다.
요약 정리
K-fold 교차 검증은 모델 튜닝/초매개변수 튜닝에 사용됩니다.
K-fold 교차 검증에는 데이터를 훈련 및 테스트 데이터 세트로 분할하고, 훈련 데이터 세트에 K-겹 교차 검증을 적용하고, 가장 최적의 성능을 가진 모델을 선택하는 작업이 포함됩니다.
이 기술에 사용할 수 있는 KFold 및 StratifiedKFold와 같은 여러 교차 검증 생성기가 있습니다.
매우 작은 데이터 세트에는 LOOCV 방법을 사용합니다.
매우 큰 데이터 세트의 경우 K 값을 5로 사용할 수 있습니다.
K = 10의 값은 K의 표준값입니다.
특히 클래스 비율이 동일하지 않은 경우 더 나은 편향 및 분산 추정치를 얻으려면 계층화된 k-fold 교차 검증을 사용하는 것이 좋습니다.
마치며
K-fold 교차 검증은 일반화 성능을 높일 수 있는 데이터 분할 방법이면서 모델 튜닝에 사용된 다는 사실을 알게 되었습니다.
그리고 K-fold 교차검증이 시계열 데이터나 너무 작은 데이터에서는 좋은 선택이 아닐 수 있다는 사실도 알게 되었습니다.
이번에는 이론만 정리했지만 실제 데이터셋에서 어떻게 적용되는지도 정리해봐야겠습니다.
그리고 공부를 하면서 K-fold 교차검증에서 파생된 LpOCV, StratifiedKFold, LOOCV, GroupKFold과 같은 여러 데이터 분할법들이 있다는 것도 알게 되었습니다.
다음에는 해당 방법들에 대해서도 공부해봐야 할 것 같습니다.
참고하면 좋은 글